Leetcode1192 Critical Coneections in a Network

Posted on In

题目描述

There are n servers numbered from 0 to n-1 connected by undirected server-to-server connections forming a network where connections[i] = [a, b] represents a connection between servers a and b. Any server can reach any other server directly or indirectly through the network.

A critical connection is a connection that, if removed, will make some server unable to reach some other server.

Return all critical connections in the network in any order.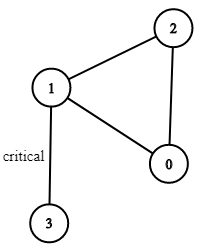


1
n = 4, connections = [[0,1],[1,2],[2,0],[1,3]]
1
Output: [[1,3]]
1
2
Explanation:
[[3,1]] is also accepted.

解析

这是Amazon OA上的一道题，可以利用Trajan算法解决，说实话，这种考法比较无聊，如果你熟悉Tarjan就能轻松秒杀，反之死活想不出来，没有什么区分度，不过既然亚麻考了这题，还是有必要熟悉下的，我OA没有碰到，但有准备过。

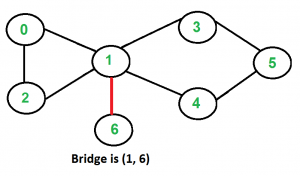
这道题目的关键是理解Bridge的含义，即连通两个连通分量的桥，根据观察我们可以发现这个Critical Connection或者说Bridge不应该出现在一个环里，Tarjan算法的核心在于，找到环，它采用了一种比较巧妙的思路，即记录每个节点第一次发现的位置，如果没有环，显然这个位置是不断增大的，如果发现某个节点可以通往比它位置小的节点则说明出现了环。

理解了这个思路，用DFS搜索图，保存第一次出现的位置和所能到达的最小位置，如果前者小于后者，则说明没有环，则这条路径是Bridge也就是Critical Connection

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
public List<List<Integer>> criticalConnections(int n, List<List<Integer>> connections) {
	int[] disc = new int[n], low = new int[n];
	// use adjacency list instead of matrix will save some memory, adjmatrix will cause MLE
	List<Integer>[] graph = new ArrayList[n];
	List<List<Integer>> res = new ArrayList<>();
	Arrays.fill(disc, -1); // use disc to track if visited (disc[i] == -1)
	for (int i = 0; i < n; i++) {
		graph[i] = new ArrayList<>();
	}
	// build graph
	for (int i = 0; i < connections.size(); i++) {
		int from = connections.get(i).get(0), to = connections.get(i).get(1);
		graph[from].add(to);
		graph[to].add(from);
	}

	for (int i = 0; i < n; i++) {
		if (disc[i] == -1) {
			dfs(i, low, disc, graph, res, i);
		}
	}
	return res;
}

int time = 0; // time when discover each vertex

private void dfs(int u, int[] low, int[] disc, List<Integer>[] graph, List<List<Integer>> res, int pre) {
	disc[u] = low[u] = ++time; // discover u
	for (int j = 0; j < graph[u].size(); j++) {
		int v = graph[u].get(j);
		if (v == pre) {
			continue; // if parent vertex, ignore
		}
		if (disc[v] == -1) { // if not discovered
			dfs(v, low, disc, graph, res, u);
			low[u] = Math.min(low[u], low[v]);
			if (low[v] > disc[u]) {
				// u - v is critical, there is no path for v to reach back to u or previous vertices of u
				res.add(Arrays.asList(u, v));
			}
		} else { // if v discovered and is not parent of u, update low[u], cannot use low[v] because u is not subtree of v
			low[u] = Math.min(low[u], disc[v]);
		}
	}
}